s4aysnek's Website

I have loved and been interested in math for a very long time by now. However, even though it may be just be my inexperience with other fields, I have found generating functions to be one of the most fascinating and thought-provoking topics I have yet learned. So what are these curious mathematical objects, and how can we solve problems with them?

Basic Definition

The most intuitive definition of generating functions I’ve heard is from Herbert Wilf’s generatingfunctionology

A generating function is a clothesline on which we hang up a sequence of numbers for display. What that means is this: suppose we have a problem whose answer is a sequence of numbers... We want to 'know' what the sequence is. What kind of answer might we expect?

… Hence the thumbnail of this blogpost.

If you’ve studied a bit of calculus and learned about power series, generating functions go hand in hand with that concept! What I mean is that we have a sequence $a_n$ . It can be any sequence of numbers. Then, the ordinary power series generating function (the opsgf) of the sequence is as follows:

Definition

A function $F(x)$ is defined to be the generating function of ${a_n}$ if

F(x) = \sum_n{a_nx^n}

Examples

If I have the sequence $\{0, 1, 2, 3, 4, 5\}$ , then the generating function for that sequence would be

$F(x) = 0x^0 + 1x^1 + 2x^2 + 3x^3 + 4x^4 + 5x^5$

You can see why Wilf alikened generating functions to clotheslines. These $x$ s are (almost) purely formal, and their only purpose is to sit there and help locate the term in the sequence.

For a more advanced example, consider the sequence $\{1, 1, 1, 1, 1, ... \}$ . This means that $a_n = 1$ for every single $n$ . So, the generating function would be $F(x) = \sum_n{1 \cdot x^n} = \sum_n{x^n}$ . But, if we recall from Algebra 2, this looks like a geometric series!

If we remember, when we have an infinite geometric series with an initial term $a$ and a common ratio $r$ , then the sum is

\sum_{n=0}^{\infty}{ar^n} = S = \frac{a}{1 - r}

In our case, $n$ starts at zero, so the initial term is just 1. $r$ in this case is also just $x$ . So, the generating function for this sequence is

F(x) = \frac{1}{1 - x}

Wait, why are we able to convert that series into that neat sum with the geometric series formula again? I thought it only converged when $|r| < 1$ We are able to do this because this is a formal power series. $x$ isn’t really a concrete number (kinda), so we can kinda do anything to it, including what we just did.

Why generating functions?

Hopefully you can kind of see the power series-like nature. However, this just looks pointless. Why did we do all of this? The reason why we did this is because for larger, more complicated problems, generating functions are easy to manipulate and can even yield you recurrance formulas, explicit formulas, and other cool things. However, when they don’t, they’re usually the next best thing, letting you extract terms with methods like the Taylor expansion we learned in calculus.

More examples

What is the generating function for $\{1, -1, 1, -1, 1, ...\}$ ? Well, this looks like a geometric sequence but every term is the previous term times -1. So, while our initial term is still 1, the common ratio is now $-x$ instead of $x$ . Plugging into the formula yields

F(x) = \frac{1}{1 + x}

Generating function operations

A reason why generating functions are so powerful is that they are really easy to manipulate. Say we’re given a sequence $a_n$ whose generating function is $F(x)$ . How do we represent $a_{n+1}$ in terms of $F$ ? As an example, if we’re given $\{0, 1, 2, 3, ...\}$ , how do we represent $\{1, 2, 3, 4, ...\}$ ?

We know that $a_n$ ’s opsgf is

\begin{aligned} F(x) &= \sum_{n \ge 0}{a_nx^n} \\ &= a_0x^0 + a_1x^1 + a_2x^2 + a_3x^3 + ... \end{aligned}

We want

\begin{aligned} ?(x) &= \sum_{n \ge 0}{a_{n+1}x^n} \\ &= a_1x^0 + a_2x^1 + a_3x^2 + a_4x^3 + ... \end{aligned}

How do we manipulate $F(x)$ into $?(x)$ ?

We can first note that dividing $F(x)$ by $x$ gets us really close. We have $\frac{F(x)}{x} = a_0x^{-1} + a_1x^0 + a_2x^1 + a_3x^2 + ...$

The only thing we’re missing is to backtrack and first eliminate that $a_0$ term so that there’s no pesky $a_0x^{-1}$ laying around. We can do this with $F(x) - a_0$ to get a final result:

?(x) = \sum_{n \ge 0 }{a_{n+1}x^n} = \frac{F(x) - a_0}{x}

An animation showing how to derive a_n+1

That’s great! But if I want to represent $a_{n+2}$ in terms of $F(x)$ ? Now that we see the general pattern, we should first eliminate $a_0$ and $a_1x$ first, then divide by $x^2$ to “shift” the series over to what we want. We end up getting

\begin{aligned} \sum_{n \ge 0}{a_{n+2}x^n} &= a_2x^0 + a_3x^1 + a_4x^2 + a_5x^3 + ... \\ &= \frac{a_2x^2 + a_3x^3 + a_4x^4 + a_5x^5 + ...}{x^2} \\ &= \frac{F(x) - a_0 - a_1x}{x^2} \end{aligned}

Definition

In general, for a sequence $a_n$ whose opsgf is $F(x)$ , the generating function for $a_{n+k}$ for any $k \ge 0$ is

\frac{F(x) - a_0 - a_1x - a_2x^2 - ... - a_{k-1}x^{k-1}}{x^k}

GenFuncs and Recursion

Armed with this knowledge, we can now tackle one of the most well-known recurrance relations in all of math: the Fibonacci Sequence.

Definition of the fibonacci sequence

A recurrance relation is an equation that defines a term by referencing other previous terms. In the fibonacci sequence, the first terms are 0 and 1, and the next term is defined by the sum of the last two terms. So, the next term is $0 + 1 = 1$ , and the next is $1 + 1 = 2$ , the next being $2 + 1 = 3$

The fibonacci sequence goes $\{0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...\}$

Mathematically, the fibonacci sequence is defined as follows:

a_{n+2} = a_{n+1} + a_n \quad (a_0 = 0, a_1 = 1)

This is great, but there is an actual explicit formula for the fibonacci sequence, meaning that there’s a formula that we can just plug in n for the nth term and get the result without recursion! Can we find it?

I mentioned that generating functions can be used to find these explicit formulas, so I’ll outline how we’ll do that, along with why we’re doing that.

The method

Step 0: Define the generating function of the sequence to be $F(x) = \sum_{n \ge 0}{a_nx^n}$

Step 1: Multiply both sides of the recurrance relation by $\sum_n{x^n}$ (i.e “multiply by $x^n$ and sum over $n$ “)

Step 2: Simplify and find $F(x)$

Step 3: Convert $F(x)$ into a series again with $x^n$ to prepare for “extraction”

Step 4: Profit

So, let’s try to tackle this!

Step 0

Looks good to me. Let’s move on

Step 1

When I multiply both sides of our recurrance relation of $a_{n+2} = a_{n+1} + a_n$ , I get

\sum_{n \ge 0}{a_{n+2}x^n} = \sum_{n \ge 0}{a_{n+1}x^n} + \sum_{n \ge 0}{a_nx^n}

Step 2

The result of step one looks very familiar… and it should! In Generating Function Operations, we talked about what the generating function would be if we “shift” $a_n$ to the right. We can just see what we did previously and plug in accordingly, also noting that $\sum_{n \ge 0}{a_nx^n}$ is the definition of $F(x)$ , leaving us with

\frac{F(x) - a_0 - a_1x}{x^2} = \frac{F(x) - a_0}{x} + F(x)

Plugging in our starting terms $a_0 = 0$ and $a_1 = 1$ simplifies the equation down to

\frac{F(x) - x}{x^2} = \frac{F(x)}{x} + F(x)

Multiplying both sides by $x^2$ yields

F(x) - x = xF(x) + x^2F(x)

Moving F(x) to one side gives us

x^2F(x) + xF(x) - F(x) = -x\\ F(x) \cdot (x^2 + x - 1) = -x

Finally, dividing yields us

Definition

The generating function for the fibonacci $F(x)$ is defined as

F(x) = \frac{-x}{x^2 + x - 1}

Step 2.5

Before we find the explicit formula, I just want to underline the fact that this generating function already works great! Remember that by definition, if we want to find $a_n$ , we look at the coefficient of $x^n$ . Recalling stuff we learned from calculus, how do we convert a function to an infinite polynomial of $x^n$ s? With Taylor/Maclaurin Expansion!

Say I wanted to find all fibonacci numbers from $a_0$ to $a_{10}$ . Because this is über impractical, I’ll ask an online calculator to help us in finding a 10th-order Maclaurin polynomial of $F(x)$ . Feel free to check for yourself on emathhelp.net

(warning: it is NOT pretty)

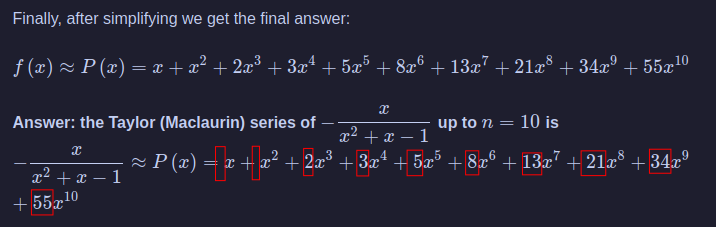
The 10th-order Macluarin polynomial for -x/(x^2 + x - 1)

Isn’t this crazy? the 0th term is defined to be 0, so it doesn’t appear in the polynomial. The 1st term is 1, so that’s why it’s just $1x$ . The second term is $0 + 1 = 1$ , so in the polynomial, there’s $1x^2$ . We are able to generate this sequence with this generating function, which is so cool already! However, let’s move on from this (incredibly important) tangent and tackle the final steps.

Is expanding with Taylor/Maclaurin a super efficient method of generating the fibonacci terms? Heck no! This just illustrates what you might do if this was your only option…

Step 3

The hardest part is probably not getting the generating function but is actually converting it into a “useable” form. When I was doing those simple generating functions in the Examples section, I used the handy infinite geometric sum

S = \frac{a}{1 - r}

I’m almost certain that we’re gonna have $x$ somewhere in our common ratio, since that’s what generating functions care about, so I’m looking for a way to convert $F(x)$ into

\frac{a}{1 - ?x}

If only there was a way to decompose my $F(x)$ into a sum of partial fractions…

Hmm? There’s something called partial fraction decomposition that does exactly that? That’s sick.

First of all, we have

F(x) = \frac{{-x}}{x^2 + x - 1}

Even though $x^2 + x - 1$ might not be factorable with integers, we can still express it as

(x - r_{+})(x - r_{-}) \\ r_{\pm} = \frac{-1 \pm \sqrt{5}}{2}

where we found $r$ with the quadratic formula. Now, let’s try to found $A$ and $B$ such that

\frac{{-x}}{(x - r_+)(x - r_-)} = \frac{A}{x - r_+} + \frac{B}{x - r_-}

Working with A, and with a shortcut, I found that

A = \frac{{-r_+}}{r_+ - r_-}

Working with B, and with the same shortcut, I found that

B = \frac{{-r_-}}{r_- - r_+}

This looks complicated until we realize that

\begin{aligned} r_+ - r_- &= \frac{1 + \sqrt{5}}{2} - \frac{1 - \sqrt{5}}{2} \\ &= \frac{2 \sqrt{5}}{2} = \sqrt{5} \\ \end{aligned}

and that

\begin{aligned} r_- - r_+ &= \frac{1 - \sqrt{5}}{2} - \frac{1 + \sqrt{5}}{2} \\ &= \frac{-2 \sqrt{5}}{2} = -\sqrt{5} \end{aligned}

By getting that

A = \frac{-r_+}{\sqrt{5}} \quad B = \frac{r_-}{\sqrt{5}}

We ultimately get

\frac{{-x}}{x^2 + x - 1} = \frac{1}{\sqrt{5}} \left( \frac{{-r_+}}{x - r_+} + \frac{{r_-}}{x - r_-} \right)

We’re getting really, really close to our goal. However, when I look at the geometric sum formula, I notice that there must be a $1 - ...$ term on the denominator. So, I’m going to try to adjust the two partial fractions until it resembles that.

\begin{aligned} \frac{{-r_+}}{x - r_+} &= \frac{{-r_+}}{x - r_+} \div \frac{-r_+}{-r_+} \\ &= \frac{1}{1 - \frac{x}{r_+}} \\ \\ \frac{r_-}{x - r_-} &= \frac{r_-}{x - r_-} \div \frac{-r_-}{-r_-} \\ &= \frac{-1}{1 - \frac{x}{r_-}} \end{aligned}

That’s better. Now, our equation is looking really nice:

\frac{{-x}}{x^2 + x - 1} = \frac{1}{\sqrt{5}} \left( \frac{1}{1 - \frac{x}{r_+}} - \frac{1}{1 - \frac{x}{r_-}} \right)

Notice how now, the partial fractions are in the form that we we original looking for. We can now do the opposite of what we did in the earlier examples and work backwards, converting from this result to a series again.

For the first result, we can see that $a$ is $1$ , and that the common ratio is $\frac{x}{r_+}$ . So, this is the same thing as

\sum_{n \ge 0}{1 \cdot (\frac{x}{r_+})^n} = \sum_{n \ge 0}{(\frac{1}{r_+})^nx^n}

Similarly, for the second result, we can see that $a$ is $1$ , while the common ratio is $\frac{x}{r_-}$ . This is now

\sum_{n \ge 0}{1 \cdot (\frac{x}{r_-})^n} = \sum_{n \ge 0}{(\frac{1}{r_-})^nx^n}

We’re getting there! Our equation looks like

\frac{{-x}}{x^2 + x - 1} = \frac{1}{\sqrt{5}} \left( \sum_{n \ge 0}{(\frac{1}{r_+})^nx^n} - \sum_{n \ge 0}{(\frac{1}{r_-})^nx^n} \right)

Finally, realizing that the two sums share the same variables and bounds, we combine the two to get a grand result of

F(x) = \frac{{-x}}{x^2 + x - 1} = \frac{1}{\sqrt{5}} \sum_{n \ge 0}{\left( (\frac{1}{r_+})^n - (\frac{1}{r_-})^n \right) x^n}

Remember that $F(x)$ is defined as $\sum_n{a_nx^n}$ . That is, the nth term of the fibonacci sequence will be the coefficient of $x^n$ What is the coefficient of $x^n$ in that giant summation we just found? Well, it’s just the stuff inside the parentheses, right, multiplied by the $\frac{1}{\sqrt{5}}$ outside, right? We are finally done.

Step 4

Definition

The nth term of the fibonacci sequence can be found with the following explicit formula:

a_n = \frac{1}{\sqrt{5}} \left( (\frac{1}{r_+})^n - (\frac{1}{r_-})^n \right) \quad r_{\pm} = \frac{-1 \pm \sqrt{5}}{2}

By doing some basic math, we find that

\frac{1}{r_+} = \frac{2}{-1 + \sqrt{5}} = \frac{1 + \sqrt{5}}{2} \\ \frac{1}{r_-} = \frac{2}{-1 - \sqrt{5}} = \frac{1 - \sqrt{5}}{2}

Giving us the more-commonly-recognized Binet’s Formula

Definition

The nth term of the fibonacci sequence can be found with Binet’s Formula:

a_n = \frac{1}{\sqrt{5}} \left( (\frac{1 + \sqrt{5}}{2})^n - (\frac{1 - \sqrt{5}}{2})^n \right)

With generating functions, we have found the explicit form of a recurrance relation with (relatively) little effort! While there are shorter, more specific proofs for Binet’s formula, this demonstrates the ease in which generating functions can manipulate sequences. I’ll talk about one more thing, then we can wrap up.

Evaluating GFs by plugging into “x”

Earlier, I said that the $x$ s found in generating functions are almost purely formal and can’t be plugged into? Well, not quite. To my understanding, despite the fact that it is a formal power series, we can still connect with the more analytical side of things and expect it to work, so long as the series converges (which we can verify with our calculus knowledge). So, let’s explore one last really cool thing about the fibonaccis and its GF.

Convergence of $F(x)$

For what values does the power series $F(x)$ converge to? If we backtrack, we remember that

\frac{{-x}}{x^2 + x - 1} = \frac{1}{\sqrt{5}} \left( \frac{1}{1 - \frac{x}{r_+}} - \frac{1}{1 - \frac{x}{r_-}} \right)

Because we know that the common ratio $r$ in an infinite geometric sequence must satisfy:

S = \frac{a}{1 - r}; \quad |r| < 1

$ $x$ needs to be convergent for both series to make sense. This gives us

\begin{aligned} -1 &< \frac{x}{r_+} < 1 \\ -r_+ &< x < r_+ \\ \frac{1 - \sqrt{5}}{2} &< x < \frac{\sqrt{5} - 1}{2}\\\\ |\frac{x}{r_-}| &< 1\\ -1 &< \frac{x}{-r_-}^* < 1 \\ r_- &< x < -r_-\\ \frac{-1 - \sqrt{5}}{2} &< x < \frac{1 + \sqrt{5}}{2}\\ \end{aligned}

* The reason why it turns negative is because $r_-$ is already negative. So, the absolute value turns it positive, which is shown by it changing signs.

From this, we can see that the stricter bound is

\frac{1-\sqrt{5}}{2} < x < \frac{\sqrt{5} - 1}{2}

which tells us that between ~ $\pm 0.61803$ , we can plug in x into

F(x) = \sum_{n \ge 0}{a_nx^n} = \frac{-x}{x^2 + x - 1}

In a sense, this relates the fibonacci sequence $a_n$ with a simple constant! One very cool thing we can do is plug in $\frac{1}{1000} = 0.001$ into x, which fits comfortably within our bounds. Something really interesting happens…

\begin{aligned} F(\frac{1}{1000}) &= \sum_{n \ge 0}{a_n (\frac{1}{1000})^n} = \frac{-0.001}{0.001^2 + 0.001 - 1}\\ &= \frac{-0.001}{-0.998999} = \frac{1000}{998999} \end{aligned}

Now let’s examine the first 50 or so digits of $\frac{1000}{998999}$

\frac{1000}{998999} = 0.001 \; 001 \; 002 \; 003 \; 005 \; 008 \; 013 \; 021 \, \\ \quad \quad \quad \quad 034 \; 055 \; 089 \; 144 \; 233 \;377 \; 610 ...

Wait, what? That simple fraction contains the first 16 fibonacci terms?? That’s really cool, but it should also not be that big of a surprise. In the equation above, we said that the fraction was equal to

F(x) = \sum_{n \ge 0}{a_n (\frac{1}{1000})^n}

Thinking about it carefully, what this is basically saying is to write down the nth term of $a_n$ , then move right 3 decimal places (since we’re dividing by 1000), then repeat. It’s kinda like a factory, churning out fibonacci terms until there’s not enough space, when the fibonacci numbers get to 4 digits and it breaks.

In many cases, we can obtain some really cool results by plugging in real (and even complex numbers!) into $x$

Conclusion

We’ve only begun to scratch the surface of generating functions, yet we’ve seen how powerful they can be. In future blogposts about generating functions, we might cover different types of generating functions, as well as even more things you can do with them, from counting to infinite sums to all sorts of cool number theory stuff. But for now, thanks for reading, and see you soon! $\blacksquare$

Generating Functions: An Intro to a Really Cool Piece of Math

Basic Definition

Examples

Why generating functions?

More examples

Generating function operations

GenFuncs and Recursion

Definition of the fibonacci sequence

The method

Step 0

Step 1

Step 2

Step 2.5

Step 3

Step 4

Evaluating GFs by plugging into “x”

Convergence of F(x)F(x)F(x)

Conclusion

Convergence of $F(x)$